MA.1
Zahl und Variable
A
Operieren und Benennen
4
Die Schülerinnen und Schüler können Terme vergleichen und umformen, Gleichungen lösen, Gesetze und Regeln anwenden.
Querverweise
MA.1.A.4
Die Schülerinnen und Schüler ...
1
a
- können unterschiedliche Anzahlen einander angleichen (z.B. 8 und 4 Knöpfe → 6 und 6 Knöpfe).
b
- können Zahlen bis 20 verschieden zerlegen (z.B. 5 = 1 + 4 = 3 + 2 = 3 + 1 + 1) und umformen (Kommutativgesetz: z.B. 5 + 3 = 3 + 5).
c
- können die Addition als Umkehroperation der Subtraktion nutzen (z.B. 18 - 15 = 3, weil 15 + 3 = 18).
- können Beziehungen zwischen Additionen mit dem Kommutativgesetz (z.B. 2 + 18 = 18 +2) und dem Assoziativgesetz (z.B. 17 + 18 = 17 + 3 + 15 = 20 + 15) nutzen.
d
- können Beziehungen zwischen Produkten nutzen (z.B. 6 · 8 ist um 8 grösser als 5 · 8 oder mit dem Kommutativgesetz: z.B. 8 · 3 = 3 · 8).
2
e
- verstehen die Division als Umkehroperation der Multiplikation und den Zusammenhang zur Addition (z.B. 28 : 7 = 4 → 28 = 4 · 7 → 28 = 7 + 7 + 7 + 7).
- können Beziehungen zwischen dem kleinen Einmaleins und dem Zehnereinmaleins nutzen.
f
- können Produkte durch Verdoppeln und Halbieren umformen (z.B. 8 · 26 = 4 · 52 = 2 · 104).
- können das Assoziativgesetz bei Summen und Produkten nutzen (z.B. 136 + 58 + 42 = 136 + (58 + 42); 38 · 4 · 25 = 38 · (4 · 25)).
- können natürliche Zahlen auf 10er, 100er und 1'000er runden.

g
- erkennen Zahlen, die durch 2, 5, 10, 100, 1'000 teilbar sind.
- können Dezimalzahlen runden (z.B. 17'456 auf 100er; 1.745 auf Zehntel).
h
- können Gleichungen mit Variablen durch Einsetzen oder Umkehroperationen lösen.
- können die Rechenregeln Punkt vor Strich und die Klammerregeln befolgen
(z.B. 4 + 8 - 2 · 3 = 6; (4 + 8 - 2) · 3 = 30; 4 + (8 - 2) · 3 = 22). - Erweiterung: können Teilbarkeitsregeln durch 3, 4, 6, 8, 9, 25, 50 nutzen und Teiler natürlicher Zahlen bestimmen.
3
i
- können ein Produkt mit gleichen Faktoren als Potenz schreiben und umgekehrt (z.B. 15 · 15 · 15 = 15³ ; a · a · a · a = a⁴).
- können das Distributivgesetz bei Termumformungen anwenden (z.B. a · (b + c) = a · b + a · c = ab + ac).
- können Rechenergebnisse sinnvoll runden.
- Erweiterung: verstehen die Konventionen über die Notation algebraischer Terme (z.B. abc = a · b · c aber 789 ≠ 7 · 8 · 9).
j
- Erweiterung: können lineare Gleichungen mit einer Variablen mit Äquivalenzumformungen lösen (z.B. 5x + 3 = 7).
- Erweiterung: können Polynome addieren und subtrahieren (z.B. 3(a² + 2b) - 2(a² + b) = a² + 4b).
- Erweiterung: können Terme ausmultiplizieren und ausklammern (Faktorzerlegung).
- Erweiterung: können Gleichungen sprachlich deuten (z.B. x = y + 1 → x ist um 1 grösser als y) und Textgleichungen umsetzen.
- Erweiterung: können Terme mit Variablen umformen bzw. sinnvoll vereinfachen (ausklammern, ausmultiplizieren, kürzen und Vorzeichenregeln).

k
- können Terme mit Variablen addieren und subtrahieren (z.B. a + 2a + b + 3b + ¼ + ⅜ = 3a + 4b + ⅝).
l
- können quadratische Gleichungen durch Faktorzerlegung lösen (z.B. x² - 4 = 0).
- können Terme mit Binomen umformen und dabei die binomischen Formeln anwenden (z.B.
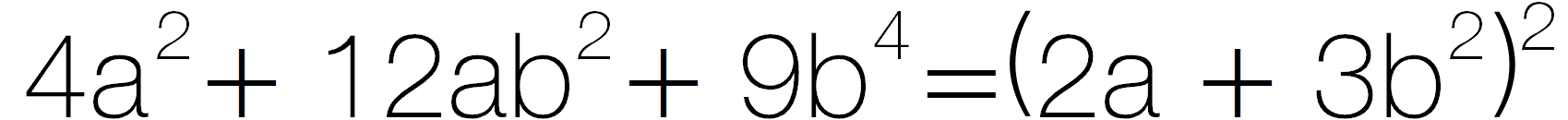 ).
). - können die Rechenregeln
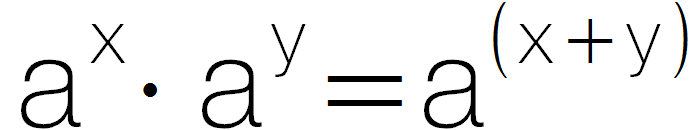 sowie Potenz vor Punkt vor Strich anwenden.
sowie Potenz vor Punkt vor Strich anwenden.
m
- können Bruchterme mit Binomen umformen.
- können Rechengesetze bei Termen mit Potenzen und Wurzeln sowie bei Zahlen in wissenschaftlicher Schreibweise befolgen.
- können Bruchgleichungen mit der Unbekannten im Nenner (z.B.
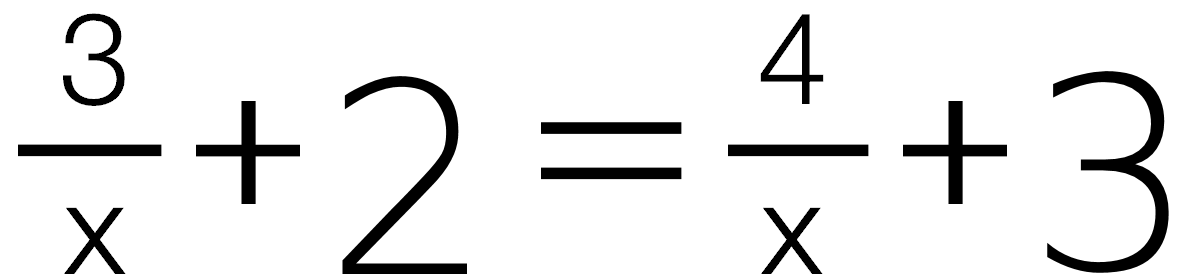 ) und Gleichungen mit einem Parameter lösen (z.B. ax + a = 7).
) und Gleichungen mit einem Parameter lösen (z.B. ax + a = 7). - können lineare Gleichungssysteme mit 2 Unbekannten lösen.



